寫完程式碼然後呢？

「大O複雜度（Big O notation）」常見7種表示演算法效率：隨著輸入數據量增加所需要的運行時間（空間消耗）
白話來說你的程式碼一旦輸入資料量超級無敵大到底要跑多久

考試來了～

linkedList = [1, 2, 3, 4, 5, ..., n]
array = [1, 2, 3, 4, 5, ..., n]

#當我訪問索引第100000000001的值，請問Linked List（連結串列）Array（陣列）各自所需時間多少？

• Linked List（連結串列）：
  「不同類型」元素（例如整數、浮點數、字符串等）
  「索引（從0開始一個跳一個記憶體空間）訪問」
  「動態變化大小」可以進行增加、刪除、修改等操作
  「一般性」資料存儲
• Array（陣列）：
  「相同類型」元素「記憶體佔用較小」
  「（直接跳）索引訪問」
  「固定大小」＋「不支持動態改變」
  「高效大量相同類型」資料存儲

解答了～

• Linked List（連結串列）「O(n)」：
  因記憶體是一個串接一個不同的位置 => 「遍歷」從index=0的記憶體空間跳到index=1的記憶體空間再到index=2最後到index=100000000001「個」記憶體空間的時間
• Array（陣列）「O(1)」：
  因記憶體分配空間是連貫一起的 => 「一次」直接跳到index=100000000001的時間
  白話來說所以數據量大就是用Array就對啦～～～～～

背下這張圖加上剛剛考試過，你就能評估你程式碼到底跑多久時間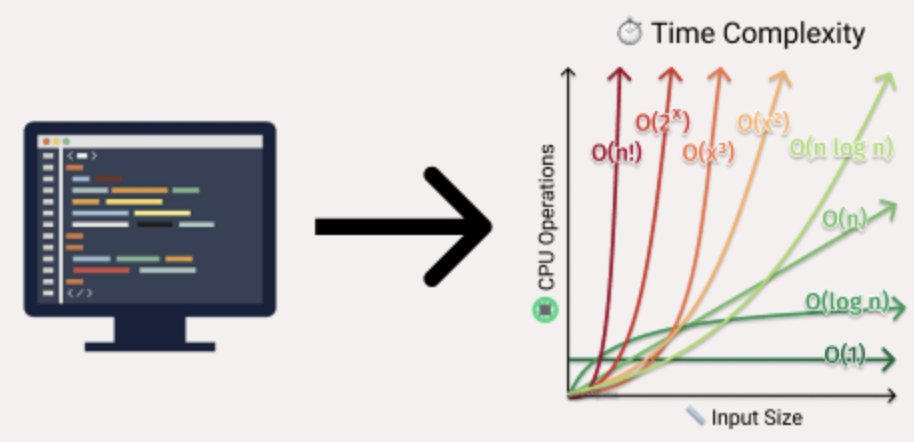

Time Complexity引用自 https://adrianmejia.com/most-popular-algorithms-time-complexity-every-programmer-should-know-free-online-tutorial-course/

O(1)  #常數時間複雜度：

不論輸入數據量的大小，算法的運行時間都保持穩定
例如：讀取一個變量、執行固定次數的運算等

O(log n)  #對數時間複雜度：

隨著輸入數據量的增加，算法的運行時間以對數方式增長
例如：二元搜索

O(n)  #線性時間複雜度：

隨著輸入數據量的增加，算法的運行時間和輸入數據量成正比
例如：線性搜索

O(n log n)  #線性對數時間複雜度：

介於線性和二次方的複雜度之間
例如：快速排序、合併排序

O(n^2)  #二次方時間複雜度：

隨著輸入數據量的增加，算法的運行時間呈平方級增長
例如：冒泡排序、選擇排序

O(2^n)  #指數時間複雜度：

當輸入數據量增加一個單位時，運行時間成倍數增加
例如：求解某些組合優化問題的暴力搜索

O(n!)  #階乘時間複雜度：

當輸入數據量增加一個單位時，運行時間成倍數增加，增長速度非常快
例如：求解旅行商問題的暴力搜索

先大概了解以上每個演算法的時間複雜度，後面幾天會一個個講到你懂啦～～